StickMetrix Bat Selector
The Swing Max Bat Selector is a database driven
application that analyses the physical properties of a
striking implement like a baseball bat and computes key
performance indicators on which a batter can rely on to
choose the most appropriate bat for his or her swing.
The model relies on extensive research carried over the
past two decades, which unequivocally point to the bat
Moment of Inertia (MOI) as the determinant factor that
drives bat speed and thus the ultimate performance of
the bat before it even strikes the ball!
Elements of anthropology have been integrated into the
model to supplement the user with actionable fitting
guidelines that relate bat performance with the batter’s
body weight.
Thus it is now possible to narrow down the selection of
a set of bats of different build specifications using the
bat BMR (Bat MOI rating) against ones’ body weight and
muscular build to yield the ONE bat amongst many with
the highest batting speed potential.
Past the ability of the StickMetrix system to predict bat
performance; the ultimate decision lies with the batter
who can best judge for him or herself of the suitability
of the bat under consideration with respect to bat
shape, material, aesthetics and other subjective
parameters. All certified BBCOR /NCAA bats being
“equal”; the Swing Max Bat Selector should prove
useful within those limits.
Bat weight:
This is the bat weight in grams or ounces as the unit
may be. Bat weight is an important consideration for
batters of all skills. Heavy bats are usually associated
with power, solid hits and fast balls but this is not
always the case.
Several “empirical” formulas were devised over the
years to aid batters select the ideal bat weight using
physiological relationships based on muscle force vs.
bat velocity and bat weight variability. Age, body weight,
pitch speed where also used to determine the ideal bat
weight. (Bahill & Freitas)
Field research conducted over the past few years has
demonstrated that a bat’s mass property; principally
weight distribution and Moment of Inertia (MOI) aka
swing weight, are far better predicators of a bat’s
kinematic potential than bat weight, since a decrease in
bat mass property strongly correlates with increased
bat velocity. (Alan M Nathan & all)
As a general guideline;
-Bat weight is not as important as weight distribution.
-Bat Weight is not as important as batting speed
-A 1.0 Mph bat speed increase yields a 5ft gain in
distance. (0.5 m/s bat speed for 1.5 m distance gain)
-While a 1 Oz. bat weight decreases swing speed by an
average 0.75 Mph.

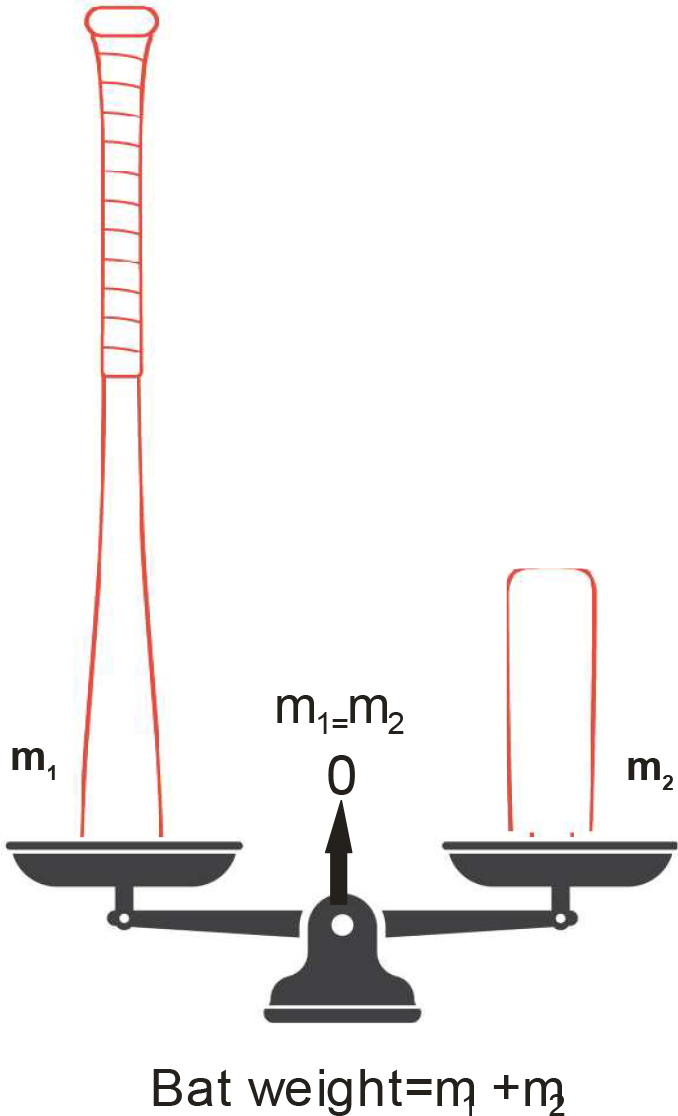
Center of Mass (CM) or Balance point:
This the distance measured from the grip end of the bat
to a point where the bat can be balanced on a knife’s
edge. The location of this point on the bat informs us
how weight is distributed between the knob end and
the barrel end of the bat.

We can clearly see that the proportions of the bat
length wise right and left of the center of the mass are
not equal. But have equal mass as if the bat was to be
cut in half at the balance point.
When the balance point (BP) is located close to the
handle (knob loaded bat), the bat can be swung faster
and slower when the (BP) is closer to the barrel end
(barrel loaded bat). Taking it to the extreme, neither a
knob loaded nor a barrel loaded bat is efficient at
transferring kinetic energy unless the ball strikes the bat
forward and in the vicinity of the balance point, usually
7~6 inch from the barrel end
General guidelines:
-A barrel loaded bat is preferable to a knob loaded bat.
-A barrel loaded bat is slower than a knob loaded bat.
-The closer the ball impact is to the Bp the more solid
the ball impact feels, and the closer the Bp is to the
barrel end the more efficient is the impact energy and
bat speed transferred to the ball.
-The further away the Bp is from the knob the higher
the bat’s swing weight and the more efficient is the
transfer of energy between bat and ball at impact.
Weight distribution Front & back (WF/WE)
The weight of the distributed between two equidistant
supports. WF &WE informs us how much of the bat
weight is distributed between the knob end and the
barrel end.
WE/WF can be determining factors when comparing
two seemingly identical bats, bats with matching weight,
and the difference between a wooden bat and a
composite / alloy bat.
WE/WF reinforce our understanding of the relationship
between weight and balance point and how to best use
weight distribution as a point of differentiation between
bats.
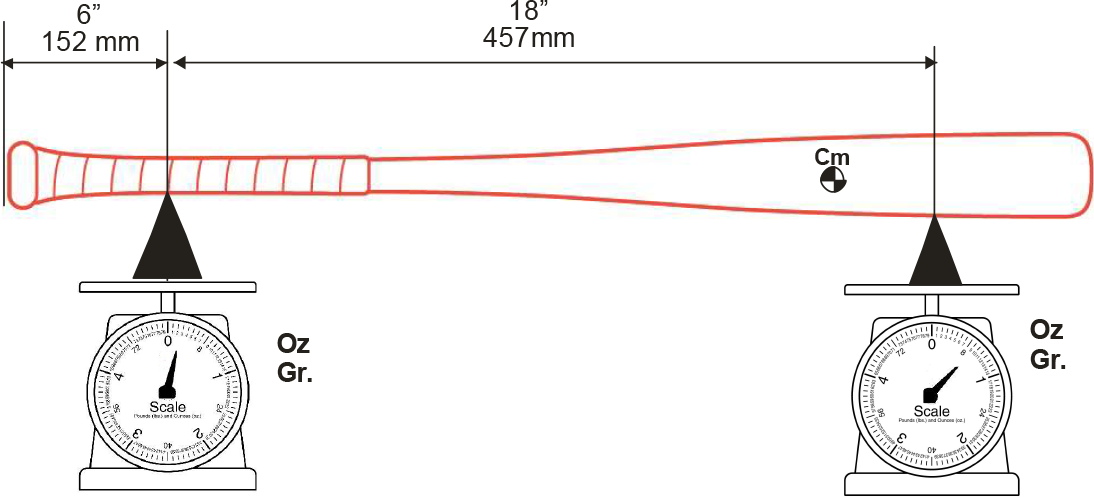
Bat Length (LN)
The bat length as measured from the knob to the barrel
end between verticals. Bat length and bat mass
property cannot be dissociated since length when
evaluated in isolation does not provide insights into the
bat’s performance.
It has to be noted however that the further away the
ball impact is from the knob end of the bat the faster
the ball. This is because the barrel tip moves at a faster
angular speed. Thus, for equal mass (weight) and
moment of inertia, the longer bat is preferred, noting
that a 1.0 Mph bat speed increase, results in a 5ft gain
in distance. (0.5 m/s and 1.5 m respectively).

Moment of Inertia (MOI) AKA swing weight:
This is the moment of inertia (MOI) of the bat. The value
is calculated based on the measured mass property of
the bat using a modified formula which gives a very
good approximation (3~10%) for MOI taken at the knob
end (Iknob) (Cross, Curtis & all)

MOI at the center of mass (Icm)
The moment of Inertia about the bat’s center of mass.
The value is calculated using the parallel axis theorem.
Icm is a very good predicator of the bat’s effective mass
Me which is the equivalent to that of a point mass when
the bat collides with the ball. (Rod Cross &all)

MOI at the handle 6 inches away from the knob (Ihandle)
is an academic convention which places the bat’s axis of
rotation at the hands and therefore on the handle.
Current research seems to indicate that Iknob and Icm are
more appropriate at predicting bat performance than
Ihandle on account of the contribution of arms and wrists
to MOI and a shift in the rotation axis which is now
much closer to the torso than originally thought.
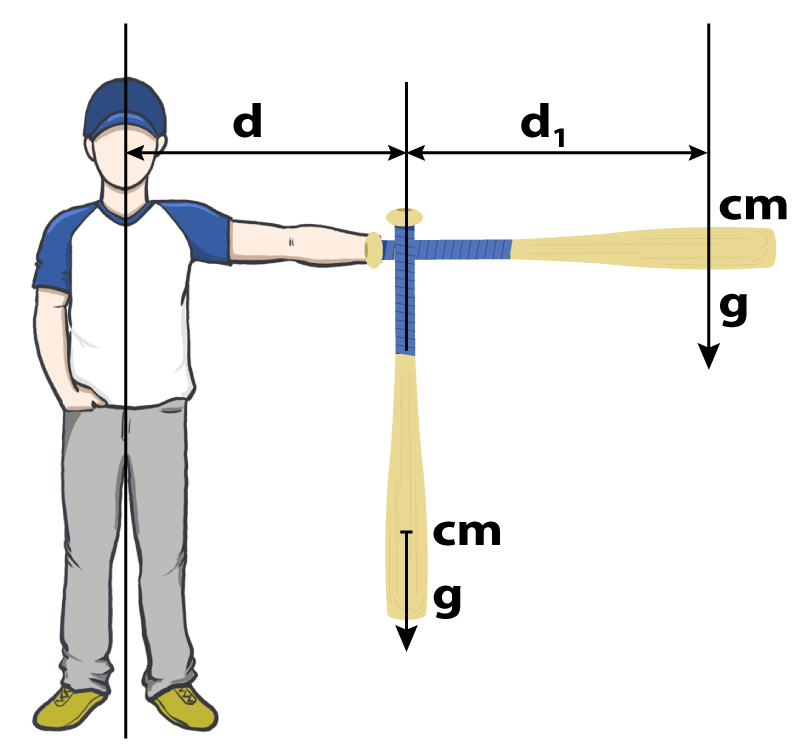
Feel Vs MOI aka Swing Weight?
Consider this first example as illustrated below; The
mass of the bat is invariant whether the it’s held at
arm’s length pointing towards the ground or when held
parallel to it. In the first case the feeling of lightness is
based on d*m and in the second case the feel of
heaviness is the product of d+d1*m. The bat will feel
lighter / heavier when d1 is decreased or increased.
In the second example, when the bat is held in our
hands at a distance d, and rotated about, some
resistance is felt. If we rotate the bat with the same
level of effort at d1 as we did at d, the bat will not move
as fast!
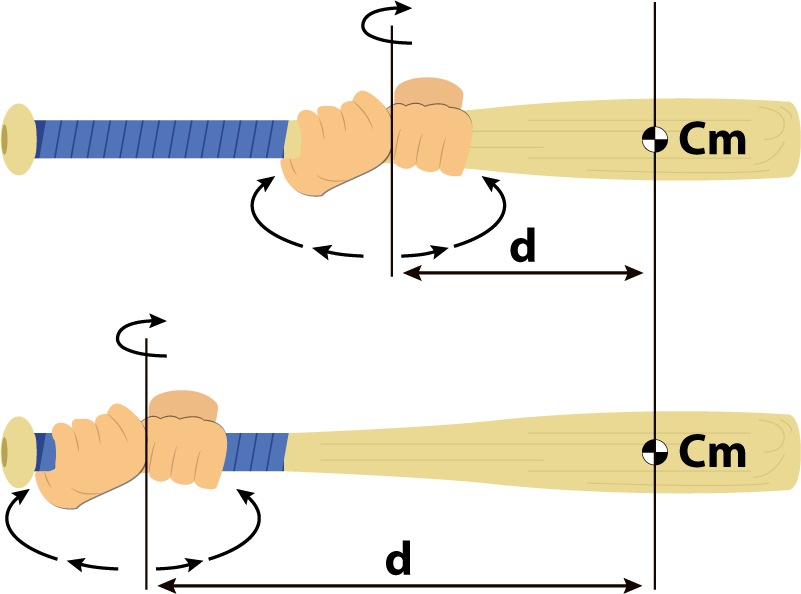
The initial resistance to our effort is the bat's inertia and
is expressed as I=mxd^2 in that the resistance to motion
increases by the square of the distance.
The concept of Feel and swing weight deal with the
same quantities for mass and distance. While feel is
static; the moment of inertia / Swing weight is an
accurate, direct correlation of the effort that must be
exerted on the bat to set it in motion at some speed.
Newton’s second law of motion lays out the relation
between torque (t), acceleration (α), moment of inertia
(I), Angular velocity (w)and kinetic energy (KE) through
the relation T=Iα and KE=½ Iw2.
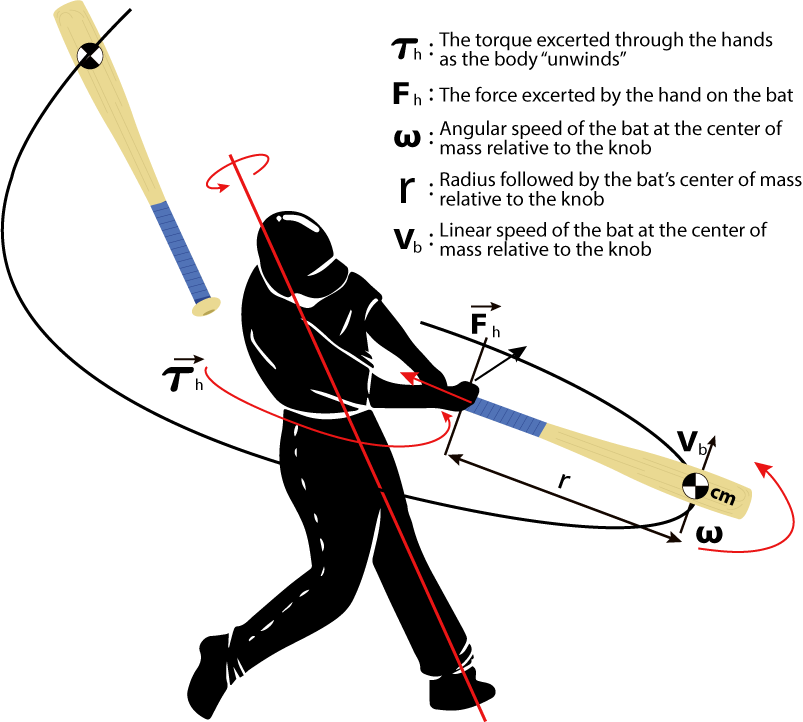
Using the standard model developed to explain the
dynamics involved; a batter must apply sufficient torque
to accelerate the bat to overcome its inertia and
achieve sufficient velocity to intercept the ball. The
ball/bat collision at speed results in the kinetic energy
that redirects the incoming ball when struck.
The model emphasis the importance of torque which
simply stated is strength. Strength is about the efficient
use of muscular mass which depending on the
individual can and often is a physical limitation that
cannot be readily overcome.
Thus, optimizing the bat MOI for the specific needs of
the batter is by far the fastest and most practical
method that would satisfy the conditions set by
Newton’s second law. T=Iα and KE= ½ Iw2)
Some facts about MOI
-A novice batter would not be able to detect a 25%
change in a bat to bat MOI comparison, while a
proficient batter would be able to detect a 2.5% change
performing the same test. (Kreifeldt and Chuang)
-Reducing bat MOI by 15% increases bat speed by 5%.
-No appreciable speed loss or gain is to be had when
the MOI differential between two comparable bats is
less than 1000 Oz^2 or 180 Kg/cm^2. When facing such
a situation the lighter and longer bat is the one to go for.
Center of Percussion (COP)
The impact point on a bat that results in the bat moving
in the same direction as the applied force, which if
applied at any other location would cause the bat to
rotate through and axis at the opposite end and in the
opposite direction.
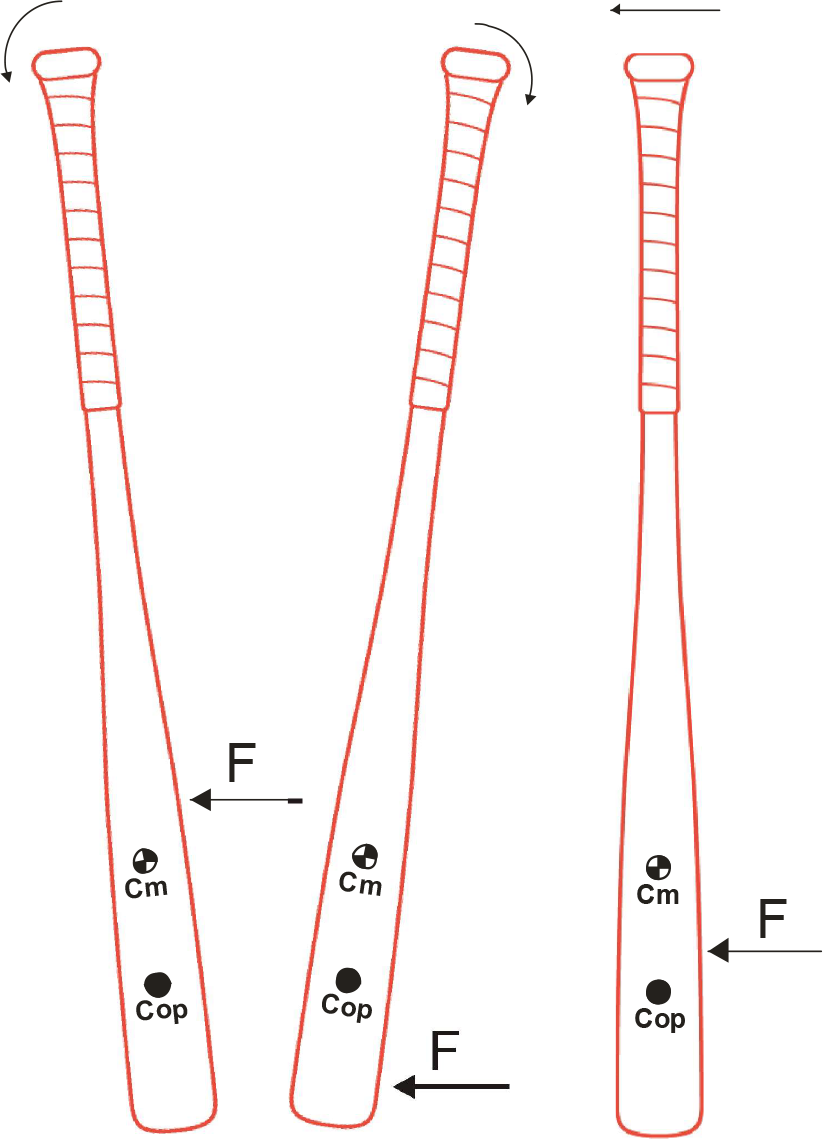

The rotation axis of an idealized impact point (cop) on
the barrel, most often than not passes through a point
that’s in the vicinity of the hands at a “theoreticaly”
assumed to be 6” from the knob end of the bat.
A recent study by (cross) postulated that the rotation
axis of the idealized cop is closer to the knob end than
first assumed because of the role the hands play in
restricting the bat during collision with the ball.
Experiments carried out for the study has also
concluded that the fundamental vibration node of the
bat lay in a region between the cop and cm, explaining
the high ball rebound velocity and the appreciable lack
of vibration, reinforcing the idea of the sweet spot
Some facts to remember when selecting a bat:
-The optimum strike zone (minimal energy loss and
highest bounce factor) is between the CM and the COP.
-The ideal strike zone is 4~10” from the barrel end.
(Crisco)
-Most bats are optimized for an impact point at or
around 6 in. from the barrel end (Cross).
-As a general rule the COP lays at a distance from the
knob about 80~85% of the bat length. (Bahil)
-Maximum batted Ball velocity drops at a rate of about
10 Mph per inch (4.5 m/s per 2.5 cm) for every strike
that falls above or below the ideal strike zone. (Crisco)
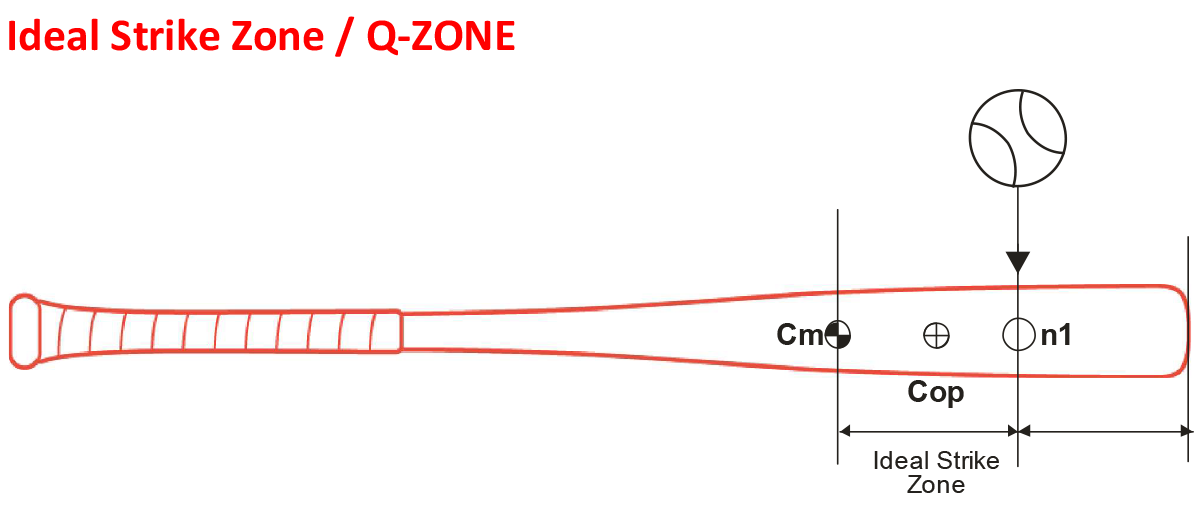
The approximate impact point on the barrel that would
result in the fastest ball exit velocity with very little
residual vibration felt in the hands of the batter. This
ideal impact spot lies in the vicinity of the fundamental
vibration node of the bat, some 5~7 inches away from
the barrel end. The use of “Q” for this region of the bat
alludes to the bounce factor which is highest between
the COP and the first fundamental vibration node.
The StickMetrix determines the Q zone based on the
mass property of the bat and the impact point on the
barre that would result in the maximum energy transfer
between bat/ball collision.
Bat Velocity Potential:
The maximum linear bat speed at or about the ideal
impact zone that could be achieved based on a
standardized swing speed function with dependency on
the bat’s inertial properties. The model is in line with
current research and provides the prospective batter
with a base line metric for picking a bat that’s a good fit
based on their current performance and bats played.
The StickMetrix calculates
Bat Maximum angular Speed in r/s. based on the
inertial properties of the bat.
Bar Maximum linear speed in m/s based on an idealized
impact point in the vicinity of the Q-zone
(Nathan)

Batted Ball Speed:
Batted ball speed is computed using the bat’s velocity
potential from its inertial properties and assumes that
the bat is .500 BBCOR compliant.
Pitched ball speed is the only user variable that may be
encountered in the field that could affect the batted
ball speed. Bats can be selected and optimized based on
the style of play, and pitch characteristics of the
opponent.
Fast pitch shortens the batter’s reaction time. This
requires a fast bat and fast acceleration, while a slow
pitch would require a slower bat to favor timing.
Note that batted ball speed holds true for either softball
or baseball and any variant in between as long as the
correct parameters are selected. Mainly ball weight,
COR and pitched ball speed.

Me, The mass fraction of the bat that directly
contributes to the bat/ball collision. The effective bat
mass is unity when the ball is truck about the CM and
decreases rapidly as the impact point moves closer
towards the tip.
The effective bat mass Aka “intrinsic power” is
calculated for the “strike zone” between the COP and
the fundamental node. The effective bat mass is less
than that of the bat. (Cross)
Recommended body Mass:
The body mass calculation ties the bat’s velocity
potential to the batter based on the bat’s inertial
properties and the conservation of angular momentum,
correlating torque and acceleration with lean body mass
for a healthy and athletic individual.
The value as derived is a starting point towards
selecting a bat that falls within the ability of the batter
and which bat can be further optimized for both power
and control instead of outright swing velocity.
As a general guideline;
-if the bat is within the weight range of batter (+/-10%);
dropping the bat inertia by 2.5~5% would result in
improved control and a better response time (bahill)
-a 10% increase in muscle mass would lead to a 3.8%
increase in bat speed. (Nathan)
Bat MOI Rating (BMR)
The performance of a baseball bat lies in its intrinsic
power and its inertial properties which dictate both the
maximum swing velocity and the potential kinetic
energy build up that can be transferred to the ball when
properly struck.
The Bat MOI Rating (BMR) correlates the combined
effect of the bat’s swing weight (MOI) on swing speed,
and the effective bat mass about the center of
percussion on the potential kinetic energy build up that
can be transferred to the ball using the relation V~1/ I0
and Me~1/M+b2/Icm (Cross & Bowers).
The BMR does not take into account the ball/ bat
collision into account since all compliant bats are
limited to a BBCOR approximating the Performance of
wooden bats and thus the BMR as formulated gives the
Prospective batter the means to differentiate between
Bats across all makes and materials using the bat’s
inertial properties and the batter’s weight class as the
only selection criteria that best suits their Physical
ability.
Drop Weight:
A popular baseball bat classification metric. The drop
weight is the bat’s weight in ounces minus its length in
inches; for example, if the bat weighs 30 ounces and the
length is 33”, the drop weight is -3.
Bats range from -3 to -13 in drop weight, with weights
closer to -3 feeling heavier and weights closer to -13
feeling lighter. This is a practical over simplification of
mass over inertia conundrum since two bats of equal
drop weight could have substantially different MOI’s.
Additionally a bat’s drop weight is too coarse of a metric
to account for subtle variations in a bat’s performance
characteristics.
|